[3]Graphs
圖形是離散數學中其中一項重要的項目。Graph的基礎介紹在DataStructures中的Graph圖形有介紹過,這裡簡單複習一些接下來會出現的基礎概念及名詞。
圖形是一種簡單用來表示成對關係(pairwise)的方法。
無向圖(Undirected graph): G
我們用V表示點nodes(vertices)的集合;E表示邊edges的集合,而每條邊都 joins 兩個點;用 Edge e ∈ E表示含有V中兩元素的子集合:e = {u,v} for some u, v ∈ V,並稱u, v 為e的兩個端點(end)。
有向圖(Directed graph): G'
我們用V表示點nodes(vertices)的集合;E'表示邊edges的集合;每個Edge e' ∈ E'都表示一個有順序的pair (u,v),也就是說u,v不可對調,並稱u是邊的頭(head)、 v 為尾(tail),另外,也稱edge e' 離開點u進入點v。
路徑Paths : P
在G=(V,E)中,有一序列P由v1,v2,....vk組成,其中每一對vi , vi+1都有邊相連。P被稱作從v1到vk的路徑,或稱為v1-vk path。若一路徑除了起點和終點外的其他點都只經過一次,就稱為simple path。
Connectivity
在無向圖中G =(V,E),若每一對(u,v)u,v∈V 都存在一路徑從u到v,則稱作connected;在有向圖中G' =(V,E')要定義connectivity則較微妙!因為可能存在u-v path但不存在v-u path,因此定義為:若每一對(u,v)u,v∈V 都存在一路徑從u到v並且存在一路徑從v到u,稱作strongly connected。
Tree
樹在DataStructures中的Tree有介紹過!若一無向圖connected且不包含cycle,就稱為tree。tree就是一種connected graph,刪除任一edge都會使其disconnect。
G是一含有n個點的無向圖,下面任兩點都保證第三點的發生:
- G is connected
- G doesn't contain a cycle
- G has n-1 edges
Connected Component
將G中所有與s相連(connected)點集合R稱作connected component,除了下面要介紹的BFS、DFS可以找到connected component外,也可以簡單用下面演算法找到:
R will consist of nodes to which s has a path
Initially R = {s}
While there is an edge (u,v) where u∈R and v∉R
Add v to R
EndWhile
correctness : 集合R最後真的是包含s的connected component of G
- 所有屬於R的點v都跟s相連 : 可由BFS保證
- 所有不屬於R的點w都不跟s相連
證明:反證法,有一點w∉R,但跟s相連。因為s∈R且w∉R,在P上必存在第一個不屬於R的點v,且v≠s。也存在一點u連到v,因為點v是第一個不屬於P的點,可知u∈R,上述可得 : 存在一edge (u,v),其中u∈R且v∉R,此敘述違反演算法中while迴圈的中止條件,矛盾。
The set of all Connected Component
任何圖中的兩點s和t,他們的connected components要不是相同就是沒交集(disjoint)。
Strongly Connected Component (SCC)
指的是一有向圖中最大的Strongly Connected子圖
Breadth-Fisrst-Search (BFS)
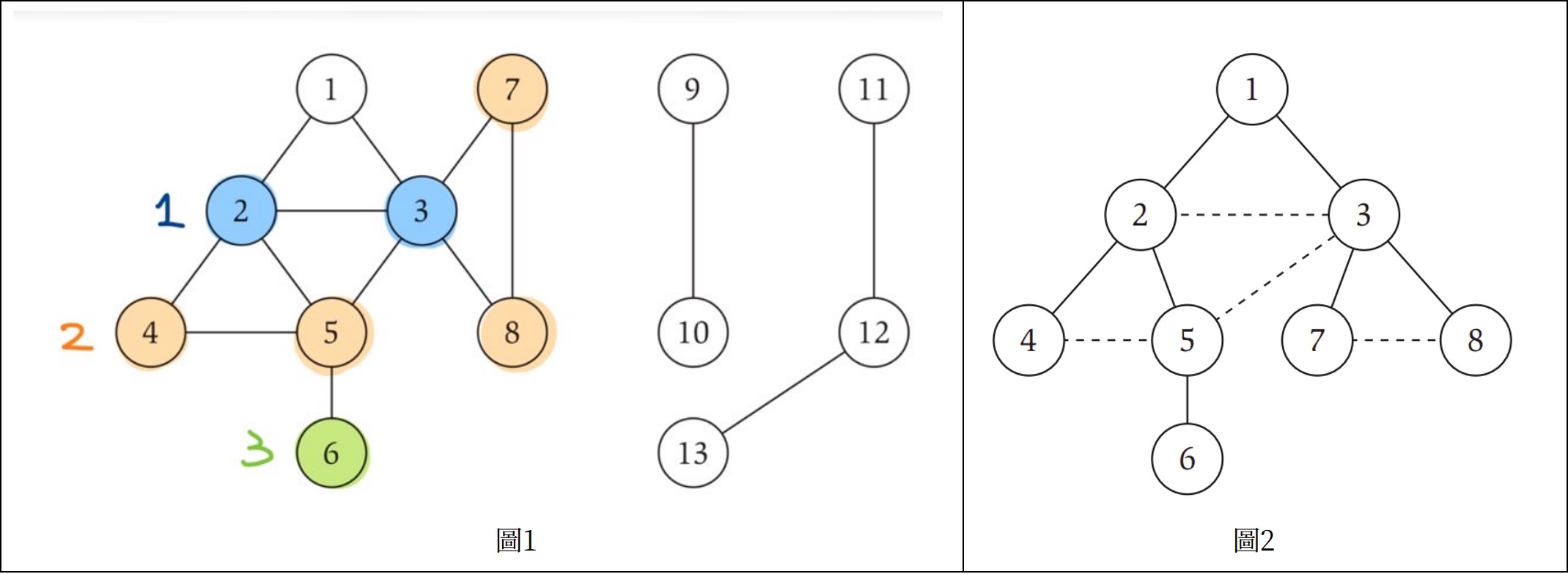
當我們要查看Graph G中的兩點s-t是否為connected時,可以嘗試用BFS演算法,以下圖1為例:以1作為s,向外尋找所有可能的方向,每次加入一層(layer),以L0(點1),L1(點2,3),L2(點4,5,7,8),L3(點6)表示。最後除了得到s可到達的點之外,也計算了到達這些點的最短距離。
*層級也可以算是一種距離的表示方式,例如點2、3距離s都是1。
其中Layer定義:
- Layer L1包含所有起點s的neighbor(為了符號的統一使用,多數時候會用L0表示僅包含起點s的集合)。
- 假設我們已經定義layers L1,...Lj,那麼Lj+1會包含所有前面層級所未包含的點,並且這些點都和Lj有邊相連。
圖1的G執行完BFS後,就會得到一棵root在s(點1)的BFS tree T,可以轉變成圖2表示,其中實線代表該edge屬於T,且當然也屬於G;虛線則代表edge屬於G,但不屬於T。
定理 :
T是一BFS tree,點x,y是T中分屬於layer Li和Lj的兩點,且(x,y)是G的一個邊。那麼i和j最多相差1。
證明 : 用反證法證明,假設i, j 相差大於1。
j>i+1,根據BFS演算法,點x的neighbor要不是在 (a)下一層,要不就是在(b)之前已經走訪過,也就是說j<i,但已假設j>i所以僅(a)成立。(a)成立也就代表j=i+1和j>i+1矛盾。
Implement
因為BFS要檢查從特定點出發可到達的點(尚未被走過的),因此可以選擇用adjacent list。另外,設一陣列Discovered[n]儲存已走過的點;陣列Li (i=0,1,2,...)儲存在第Li層的點,其中L[i]用stack和queue都可以,因為和順序沒關係。
O(m+n)
BFS(s):
Set Discovered[s] = True and Discovered[v]=False for all other v
Initialize L[0] to consist of the single element s
Set the layer counter i=0
Set the current BFS tree T = ∅
While L[i] is not empty
Initialize an empty list L[i+1]
For each node u∈L[i]
Consider each edge (u,v) incident to u
If Discovered[v] = false then
Set Discovered[v]=true
Add edge (u,v) to the tree T
Add v to the list L[i+1]
EndIf
EndFor
Increment the layer counter i by one
EndWhile
Depth-Fisrst-Search (DFS)
類似老鼠走迷宮:選定一條可走的邊之後會一直走到走不下去為止,再回頭找到之前沒探索過的點繼續走。
DFS(u):
Mark u as "Explored" and add u to R:
For each edge (u,v) incident to u
If v is not marked "Explored" then
Recursively invoke DFS(v)
EndIf
EndFor
剛剛圖1(下圖3)若改成DFS,執行過程就會像圖4一樣。
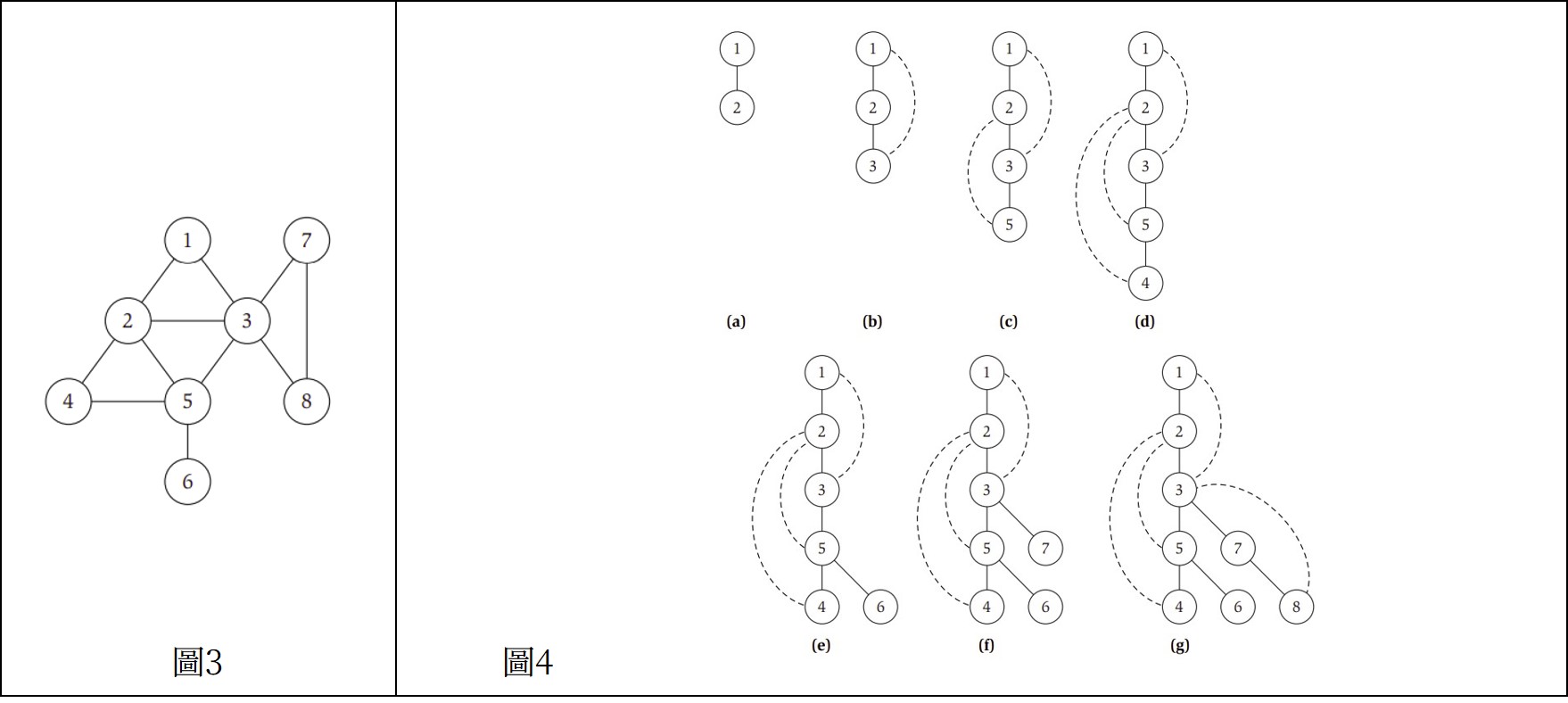
可觀察到在遞迴呼叫DFS(u)時和遞迴呼叫結束之間的所有點都會是已被標註"Explored"的點(如點u)的後代。
定理 :
T是DFS tree,x, y是T中的兩個點且edge(x,y)屬於G但不屬於T。那麼x,y其中一個會是另一個的祖先。
證明 : WLOG, 在DFS演算法中,x比y早被走到,當查看與x相連的y時,因為edge(x,y)不屬於T表示y並未被標示成Explored。因為在第一次呼叫DFS(x)時,y未被標記成Explored,代表這個點是在遞迴呼叫DFS(x)和遞迴呼叫結束之間發現的,因此我們可以由上面的觀察知道y是x的後代。
*WLOG : Without Loss of Generality不失一般性
Implement
用一陣列Explored[n]存走訪過的點;Stack(LIFO)存要被檢查的點。
O(m+n)
DFS(s):
Initialize S to be a stack with one element s
While S is not empty:
Take a node u from S
If Explored[u] = False then
Set Explored[u] = true
For each edge(u,v) incident to u
Add v to the stack S
EndFor
EndIf
EndWhile
Bipartiteness
Bipartitie graph (bigraph)G = (X,Y,E) ,G當中的所有點可以被分為兩個集合X, Y,且每一條邊一端點位於X、一端點位於Y。X和Y是兩個不相交的集合。X,Y內的任兩點不相鄰。圖5。
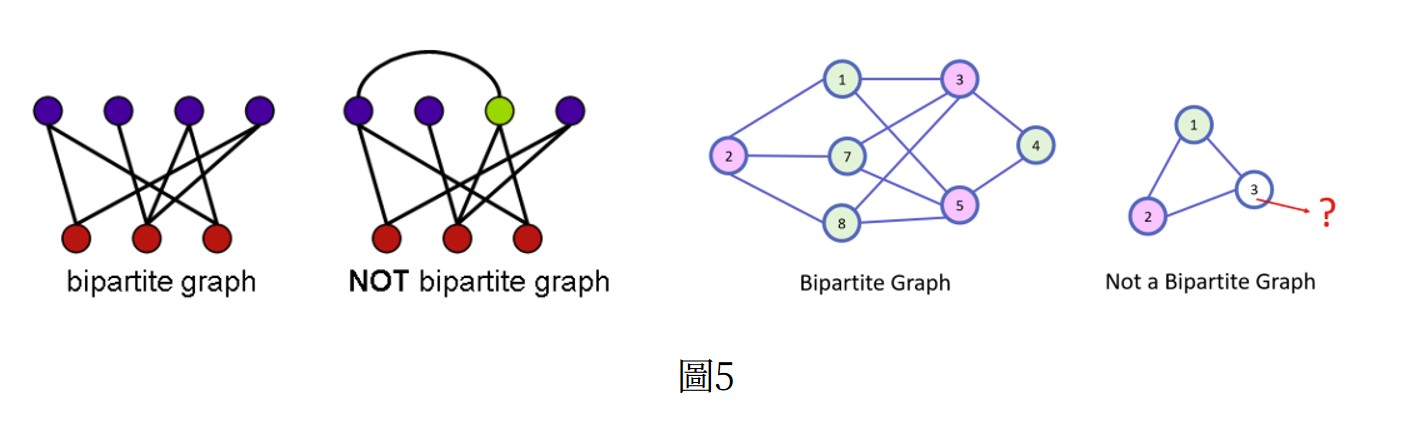
If a graph G is bipartite, then it cannot contain an odd cycle.
Test Bipartiteness
我們知道bigraph中的每一條邊都連接不同集合的點,想像成將一端點塗為紅色、另一端點塗為藍色,那麼我們可以BFS的演算法來完成:從點s出發,遇到另一點就將其塗為紅色,遇到下一點再塗為藍色,再換回紅色....;或者也可以說是將點s塗為紅色、L1塗為藍色、L2塗為紅色...。
再查看一次一般的BFS演算法。加上陣列Color[v]儲存每一點的顏色,當點v 被加入陣列L[i+1]時,若i+1為偶數則塗成紅色;奇數則塗為藍色,最後我們在檢查每條邊是否兩端都被塗上相異的顏色。時間複雜度和BFS一樣為O(M+N)。
BFS(s):
Set Discovered[s] = True and Discovered[v]=False for all other v
Initialize L[0] to consist of the single element s
color[s] = red
Set the layer counter i=0
Set the current BFS tree T = ∅
While L[i] is not empty
Initialize an empty list L[i+1]
For each node u∈L[i]
Consider each edge (u,v) incident to u
If Discovered[v] = false then
Set Discovered[v]=true
Add edge (u,v) to the tree T
Add v to the list L[i+1]
If i+1 is even then
color[v]=red
Else
color[v]=blue
EndIf
EndIf
EndFor
Increment the layer counter i by one
EndWhile
Correctness :
G是一connected graph,以s做為起點運用BFS產生layer L1,L2,....。那麼下面至少有一項成立:
- G當中不能有邊上兩點在同一層,使得G為bipartite
- G當中有邊上兩點在同一層,那麼G含有odd-length cycle,使得G不為bipartitie
第二點證明:
假設存在一edge(x,y)且x和y屬於同一層 Lj。令z = lca(x,y) [lca : Lowest Common ancestor]且點z位於Li。考慮一cycle : (x-y),(y-z),(z-x)那麼x-z這條路徑長度就是1+(i+j) +(i+j) ,為一odd cycle。
Connectivity
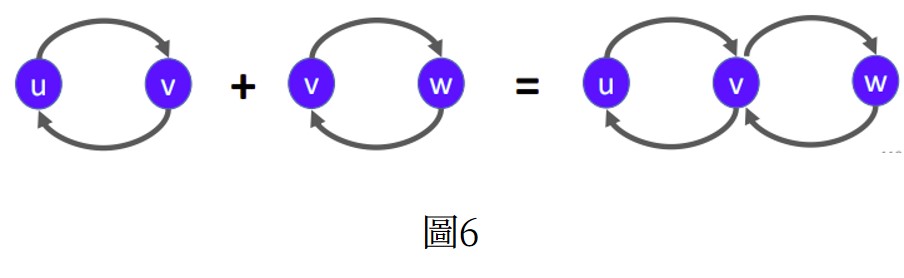
Strong connectivity指在有向圖中存在pair (u,v) 其中有u-v path也有v-u path,也稱u,v是mutually reachable。mutually reachable有一些很棒的特性,且大部分出自下面這個簡單的事實:
若u, v 是mutually reachable,v,w 是mutually reachable,那麼u,w也是mutually reachable
證明 :
Testing Strong Connectivity
是否能以linear time檢查一graph是不是Strong Connectivity?
白話來說,跑兩次BFS就可以!因此時間也為O(n+m)
其中Grev為將G中所有edge方向反轉。
TestSC(G)
Pick any node s in G
R = BFS(s,G)
Rrev = BFS(s,Grev)
If (Grev = V = R) then
return true
Else
return false
Correctness
(1) Not strongly connected(return false)的正確性:
以BFS對G及Grev 以點s為起始搜尋,若任一搜尋無法到達每一點,即違反strongly connected的定義,那麼此圖G必定不為strongly connected。
(2) strongly connected(return true)的正確性:
以BFS對G及Grev 以點s為起始搜尋,s可到達每一點且每一點也能到達s,代表s到任一點u是mutually reachable,到任一點v也是mutually reachable,根據上面的定理可得在G中的任一兩點皆為mutually reachable,符合strongly connected的定義。
Directed Acyclic Graphs and Topological Ordering
Directed Acyclic Graphs 簡稱為DAG,代表一有向圖中不包含cycle。若一無向圖不包含cycle那麼它就有非常簡單的結構,每個connected components都是一棵樹;在有向圖中沒有cycle可能也具有豐富的結構性,例如擁有較多邊的圖(圖7)。
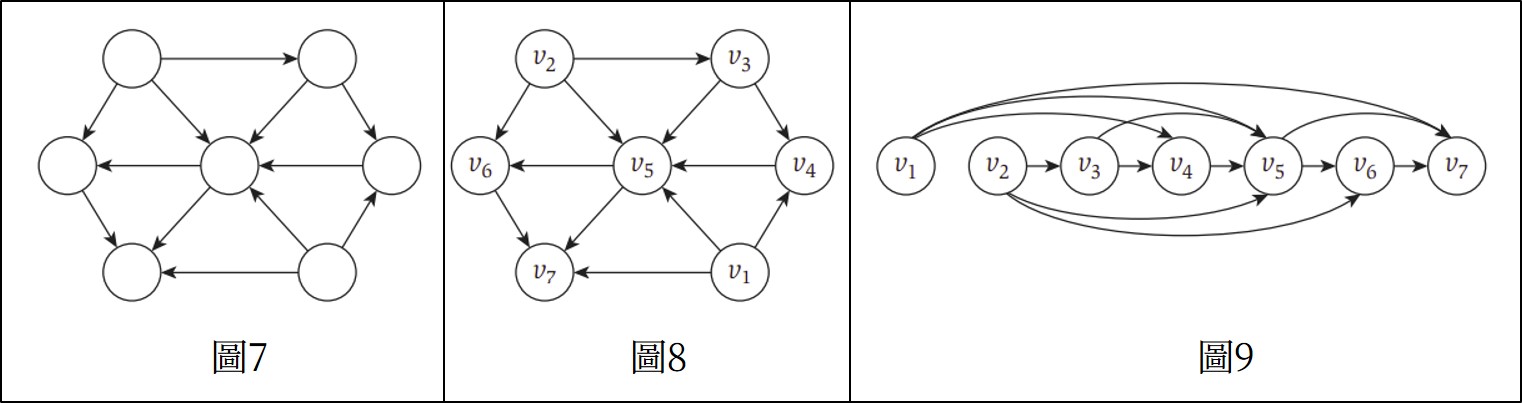
DAG可以用來表示 前後順序關係或 依賴性(dependencies),是電腦科學中常見的結構,我們可以將圖7編號變成圖8。進一步討論 前後順序關係,日常生活中像是修課的順序,需要先完成某項課程才能選修進階課程這樣的作法,必須由較小的點在前往較大的點,稱為topological ordering,圖9就是一種,也是圖8所轉換而來的。
定理 :
若一graph G為topological ordering,那麼G是一DAG
證明 :
以反證法證明,G為一topological ordering : v1,v2,...,vk且含有cycle C。令vi為C中擁有最小index的點,vj是vi前的點(有一edge(vj,vi))。要選擇vi時,代表我們已經選過vj,和G為topological ordering 的假設矛盾。
Q:若G為一DAG, 那麼G會有topological ordering嗎?
定理1 :
在每一個DAG G中,都至少存在一點沒有流入的邊
證明 :
用反證法證明,G是一DAG,且每一點都至少有一流入的邊。
選一點v,因為有回去的邊所以一定可以往回找到一點u,到u之後一定也可以往回找一點x,如此往回找的動作重複n+1次後(一開始找v也算一次),因為總共只有n個點,所以會找回第一個點v,也就代表存在cycle,和DAG的定義矛盾。
有了定理1就可以回答這個問題。
定理2 :
If G is a DAG, then G has a topological ordering.
證明 :
用歸納法。
我們可以聲稱 "每一DAG都有topological ordering",尤其在點個數為1和2時更為顯而易見。現在聲稱在有n個點時仍為真,給定一G有n+1個點,必定能找到一點v沒有流入的邊(定理1),將v放在topological ordering的第一位是可行的,因為v的邊都是流出的,現在G - {v}仍是DAG,因為不會形成cycle(n個點的G本來就沒有),所以我們可以得到topological ordering : G - {v},並將這些點放在v後面,這些在G當中所有邊都有流向的地方(順序關係),因此這是一個topological ordering。
Compute a topological ordering of G
根據上面的定理,可以設計出下面的演算法。 並且根據此演算法,將上面圖8轉為圖9的過程如下圖10所示。
To compute a topological ordering of G:
Find a node v with no incoming edges and order it first
Delete v from G
Recursively compute a topological ordering of G−{v} and append this order after v

時間複雜度
找到沒有流入的點v並且自G中刪除需要O(n)的時間,共要執行n次,所以是O(n^2)。當G非常稠密(dense),含有Θ(n^2)個邊時,這樣的時間複雜度對於輸入大小來說是linear;但是當邊(m)的數量大幅小於點(n)的數量,若時間複雜度為O(m+n)會是O(n^2)大幅的改善。
我們可以藉由「疊代(iteration)刪除沒有流入的點」的方式達到O(m+n)。若一點尚未被演算法刪除,宣告為"active",並且維持下面兩件事:
- 對每一點w維持「是從active點流入的邊」的數量
- 一集合S包含G中所有「沒有從其他active點流入的邊」的active點
起初所有點都是active,所以可以很好初始化上面兩點。接者每一疊代都從S挑出一點v並刪除,刪除v後查看所有與v有邊的點w,若邊的流向為v->w則將w「是從active點流入的邊」的數量減1,當數量為0時,將w加入集合S。藉由這樣的方式,可以持續找到有資格被刪除的點,並且在過程中用constant work在處理邊上。